Autumn 2020 Newsletter

Autumn 2020 Newsletter
Issue 176
Due to the coronavirus pandemic this meeting was cancelled and was held ‘virtually’ online via Google Meet.
At around 2:00pm we had a short committee meeting, followed by the Model Tour in which members were invited to give a short talk about their models — in particular their entries for the Secretary’s Challenge!
Written by Richard Marsden
Not a lot more, I promise.
In my earlier article I referred to Pythagoras’ theorem, and how it could be used to create right-angled triangles from standard Meccano strips or girders.
It turns out there is another rule, Ptolemy’s Theorem, which is just as useful. I’d never heard of it until I saw it in a Numberphile video on YouTube (a series I heartily recommend, by the way). It certainly wasn’t taught to me at school. This is probably because it is much trickier to prove than it is to state, so I’ll just state it.
Watch Numberphile’s video on Ptolemy’s Theorem
Ptolemy’s theorem applies to quadrilaterals — shapes with four sides — that have all four corners lying on the same circle. In this case, the product of the quadrilateral’s two diagonals equals the sum of the products of the pairs of opposite sides. Sounds a bit like Pythagoras, doesn’t it?
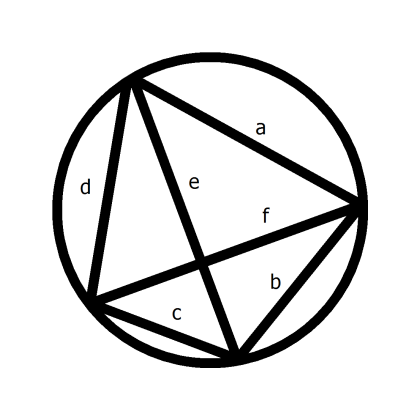
Figure 1 General quadrilateral on a circle
So, looking at Figure 1:
a × c + b × d = e × f
In fact, if the quadrilateral is a rectangle, because of the rectangle’s symmetry, it can be shown that Ptolemy reduces to Pythagoras. In other words, Pythagoras is a special case of Ptolemy, which is therefore the wider theorem. Move over, Pythagoras!
Where it becomes useful to us is in building a tapering tower with cross-bracing, with every piece an exact multiple of half-an-inch. (The usual rule applies of lengths being measured between end-hole centres as opposed to overall lengths, and, as just noted, in half-inch multiples).
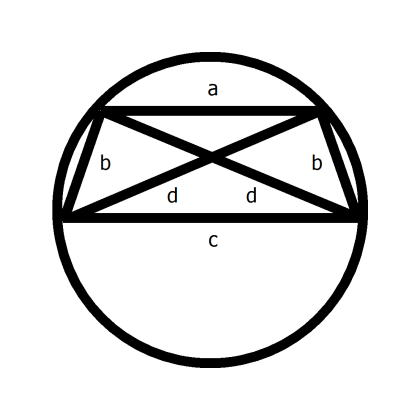
Figure 2 Quadrilateral with two parallel and two equal sides
Referring to Figure 2, our tapering section is a quadrilateral with two parallel unequal sides, being the top and bottom, the other two sides being the same length.
By symmetry, this shape will sit with all four corners on a circle, so Ptolemy applies. I’ve drawn the quadrilateral as being wider than it is tall, but it doesn’t have to be.
Because the diagonals are also the same length as each other:
a × c + b × b = d × d
Or, applying a bit of school algebra:
a × c = d² – b² = (d – b) × (d + b)
So you could simply make a = d – b and c = d + b
However, this will simply give you a flat shape with all four corners on the same straight line, on a circle of infinite radius. So you need d – b and/or d + b not to be prime numbers so you can swap factors from one to the other, to give you a more convenient shape.
Examples are 7 (top), 8 (bottom), 5 (sides) and 9 (diagonals), and 9, 12, 6 and 12. The first is based on d = 9 and b = 5 with a factor of 2 swapped between a and c. The second is d = 4 and b = 2, again with a factor of 2 swapped across, and the whole thing tripled. Indeed, you can double, triple, and so on, any of the sets of numbers and it will still work. See the close-up photograph of one of my models below for these examples in practice.

Ptolemy’s Theorem in action in a model
Beyond this, other examples can be found ‘by inspection’, as my maths master used to say with unshakeable optimism.
A slight drawback is a that lengths don’t always work out to match standard strips, so you need to build up from smaller ones (or trim longer ones with a hacksaw, not that you would of course). Also, I can’t find an example where the diagonals are split into two integer halves, so you can drop in a bolt exactly at the crossing point, and it may be that it never happens. Is there a proof either way? An exercise for the reader perhaps.
On the plus side (no pun intended), there may be some near-miss combinations, where the perforations line up closely enough for the bolts to slip in (like 15, 26, 30 for a right-angled triangle). I don’t know; I haven’t looked yet, but I’d expect them to be quite large.
In all, a useful bit of maths. I’m just surprised I didn’t come across it sooner.